How EM (Expectation Maximization) Method Works for Clustering

Background

To get strong understanding about EM concept, digging from the mathematical derivation is good way for it. But before it, let’s put the condition first. EM method is intended for clustering, and the most familiar method is k-means clustering, which is the special case of EM method that use Gaussian mixture to model the cluster areas and using hard clustering instead of soft clustering.

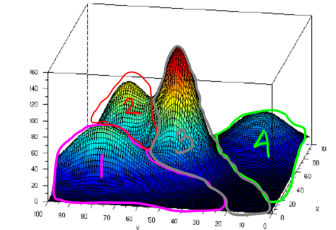
See picture below.

Picture above shows that we have 4 clusters where each cluster is modeled using Gaussian. To determine the data belongs to which cluster, we can just determine by finding the maximal value among the fourth Gaussian value. The data will be clustered to the cluster whose Gaussian value is maximal in that location. For instance, the area in the pink line boundary has maximal Gaussian value which is from Gaussian value in cluster 1, likewise for other clusters. Doing this type of clustering, the clustering boundary may intersects each others and taking cluster whose the value is maximal, is called soft clustering. Whereas for hard clustering, the boundary doesn’t intersect each others. To be able to cluster like that, we need parameters mean and variance of all those 4 Gaussian distributions, given data set input without class label. And we can achieve this by using EM method.

Deriving Gaussian Distribution

Gaussian is very important distribution. During this post, we will discuss the detail of Gaussian distribution by deriving it, calculate the integral value and do MLE (Maximum Likelihood Estimation). To derive Gaussian distribution, it is more difficult if we do it in cartesian coordinate. Thus, we will use polar coordinate. Before we derive the Gaussian using polar coordinate, let’s talk about how to change the coordinate system from cartesian to polar coordinate system first.

(1) Changing coordinate system from cartesian to polar coordinate

Changing coordinate system from catersian to polar coordinate is useful, such as when we calculate integral of certain function, in certain case, we prefer to use polar coordinate system because it will be away easier to calculate. To do that, we can use Jacobian matrix. Jacobian matrix actually defines partial derivative of a vector with respect to another vector. In our case changing cartesian coordinate to polar coordinate, the Jacobian matrix of in cartesian coordinate with respect to in polar coordinate is: